-
[python] ARIMA 데이터 생성 및 모형 적합 절차카테고리 없음 2020. 3. 18. 22:35
ARIMA(p,d,q)모형은 차수 p,d,q의 값에 따라 다른이름으로 불린다. p는 AR모형과 관련된, q는 MA모형과 그리고 d는 시차와 관련된 파라미터 이다.
ARIMA의 모수는 크게 3가지가 있다. AR모형의 Lag을 의미하는 p, MA모형의 Lag을 의미하는 q, 차분(Diffrence)횟수를 의미하는 d 가 그것이다. 보통은 p, d, q의 순서로 쓴다.
@ 정상성: 시간의 추이에 관계없이, 평균과 분산이 균일함
예1) d=0이면, ARMA(p,q)모형이라 부르고 이 모형은 정상성을 만족한다.
예2) p=0이면, IMA(d,q)모형이라 부르고 d번 차분하면 MA(q)모형을 따르게 된다.
예3) q=0이면, ARI(p,d)모형이라 부르며, d번 차분한 시계열이 AR(p)모형을 따르게 된다.
이번에는 직접 Python을 통해, 차분 d가 0인 ARIMA(p,q) 데이터를 생성해보겠다.
arma_generate_sample 모듈을 사용하여 AR, MV 파라미터 값만 조절하면, ARMA 데이터를 생성할 수 있다.

현재 ARMA 데이터를 생성해보았다. 이때 ARMA(P,Q) = AMRA(AR,MV)에서 파라미터 값을 어떻게 정할까. 모형 적합 절차에서 ARMA 모형 적합 절차라고 하는 것은 ARMA(P, Q)에서 P, Q를 잘 선택해 가장 적절한 모형을 찾는 것이다.
일반적으로 P,Q 를 간결의 원칙에 따라, P <3 , Q < 3으로 선택하는 것이 이상적이다. 모형 개수가 증가하면 예측 모형이 복잡해질 뿐 아니라 추정의 효율성도 떨어지기 때에, 모수의 개수가 적은 모형이 좋다.
또한, p + q < 2, p x q = 0 인 값들을 많이 사용한다. (둘중 하나의 모수가 0이라는 것은 실제로 대부분의 시계열 자료에서는 하나의 경향만을 강하게 띄기 때문에, 하나의 모수를 0으로 설정한다)
차분 d의 경우 정상성(트랜드가 없는 상태)을 만족시키는 만큼 차분해주면된다. ARIMA는 비정상 시계열 데이터를 차분을 통해, 정상성을 만족시키도록 한다.
가장 먼저 p와 d의 적합성을 파악하려면 ACF, PACF의 그래프를 확인해보는 것이다.
ACF는 자기상관계수, AutoCorrelation Function 으로 k기간 떨어진 값들의 상관 계수이고
PACF는 부분(편) 자기 상관 계수, Partial ACF로서 서로 다른 두 지점 사이의 관계를 분석할때, 중간에 있는 값들의 영향을 제외시킨 상관계수 이다.
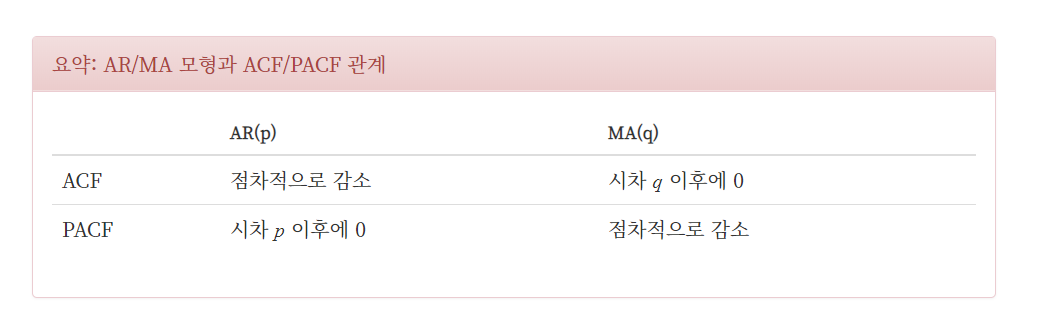
AR,MA를 지정한뒤 ACF와 PACF의 그래프를 그려보면 ARMA모형의 적합성을 판단할 수 있다.
모델 적합성의 가장 큰 증거는 ACF가 점차 감소하는 모습을 띄는 것이다.


앞서 생성한 ARMA데이터에 대하여 ACFR, PACF를 그려보면 다음과 같다. 그래프를 해석할때, lag(x좌표) =0 인 지점은 읽지 않고 어느 지점 부터 구간안에 들어가는지를 파악하면 된다. ACF가 lag=4에서 절단점을 가지고(절단점-1= 3 = q), PACF는 LAG가 4(절단점 -1 = p=3)이후에 절단점을 가진다.
따라서, ARMA(3,0) 혹은 ARIMA(0,3) 모델을 추측해볼 수 있다.
참고: PACF를 통한 시차 d 파악